What is Inertia – जड़त्व क्या है? आसान भाषा में समझें

What is Inertia? क्या आपने कभी सोचा है कि जब कोई चलती हुई बस अचानक रुकती है तो यात्री आगे की ओर झटका क्यों महसूस करते हैं? इसका कारण है जड़त्व (Inertia). What is Inertia का सीधा उत्तर है — यह किसी वस्तु की वह प्रवृत्ति है जिसमें वह अपनी गति या विश्राम की स्थिति को बनाए रखती है और इसमें होनेवाले कोई भी बदलाव को विरोध करती है . यह एक शक्तिशाली और अद्भुत भौतिक गुण है जो हमारे आसपास की हर वस्तु पर प्रभाव डालता है.

हम इस लेख में समझेंगे कि जड़त्व क्या होता है, इसके प्रकार, दैनिक जीवन में इसके प्रभाव, और क्यों यह न्यूटन के प्रथम गति नियम का मूल आधार है . आइए विज्ञान की इस रोचक यात्रा की शुरुआत करें! .

What is Inertia: जड़त्व क्या है?

अगर सरल शब्दों में समझाना हो कि जड़त्व क्या होता है, तो हम इसे कुछ इस तरह कह सकते हैं. कोई भी वस्तु अगर गति में है तो वो उसी स्पीड उसी दिशा में आगे जाना पसंद करती है . अगर वस्तु विश्राम अवस्था में है तो वो उसी अवस्था में रहना चाहती है . अपनी अवस्था में होने वाले किसी भी बदलाव को वस्तु विरोध करती है . वस्तु के इसी गुण को inertia कहते .

जड़त्व और द्रव्यमान का संबंध (Relation Between Inertia and Mass)

सभी वस्तुओ में inertia का गुण होता है . यानी सभी वस्तु अपने गति में होने वाले बदलाव को विरोध करती है . लेकिन अलग अलग वस्तु अलग अलग मात्रा ये विरोध करती है . कौनसी वस्तु कितने मात्रा में विरोध करेगी ये उसके द्रव्यमान (mass) पर निर्भर करता है . अगर (mass) द्रव्यमान ज्यादा हो तो वस्तुए अपने गति में होने वाले बदलाव को विरोध भी ज्यादा करती है . अगर द्रव्यमान कम हो तो गति में होने वाले बदलाव को विरोध भी कम होता है .

गति का पहला नियम और वस्तुओं का जड़त्व (Newton’s First Law and Inertia Explained)

न्यूटन का पहला नियम और inertia दोनों में काफी समानता है . न्यूटन के पहले नियम को law of inertia भी कहते है . न्यूटन का नियम कुछ ऐसा है . ऑब्जेक्ट अगर विश्राम स्थिती में है तो वो विश्राम स्थिती में ही रहेगी . या ऑब्जेक्ट कुछ स्पीड से किसी दिशा में जा रही है तो वो उसी स्पीड से उसी दिशा में जाती रहेगी , जब तक उस पर कोई बाहरी बल नहीं लगता तब तक .

यहाँ पर एक चीज के ओर ध्यान देना जरुरी है की inertia कोई फोर्स (बल ) नहीं है . बल्कि inertia ऑब्जेक्ट का गुण है . जो ये तय करता है की ऑब्जेक्ट (वस्तु ) फोर्स को कितना विरोध करेगी .

जडत्व के उदहारण (examples of inertia in daily life)

1) जब कोई बस या कार तेज़ी से चल रही होती है और अचानक ब्रेक लगता है, तो हमारे शरीर का ऊपरी भाग आगे की ओर झुकता है . इसका कारण है Inertia of Motion (गति का जड़त्व) — शरीर अपनी गति को बनाए रखना चाहता है.

2) ज़मीन पर रखी फुटबॉल तब तक वहीं रहती है, जब तक आप उसे पैर से नहीं मारते . इसे विश्राम का जड़त्व कहते हैं — जब कोई वस्तु रुकी हुई होती है, तो वह अपनी स्थिति में बनी रहना चाहती है .

3) जब आप पंखे को बंद करते हैं, तो वह तुरंत नहीं रुकता — कुछ समय तक धीरे-धीरे घूमता है . इसका कारण है गति का जड़त्व — पंखा अपनी गति को बनाए रखने की कोशिश करता है .

4) एक भारी बॉक्स को धक्का दिए बिना वह अपनी जगह से हिलता नहीं . यह विश्राम का जड़त्व है — वस्तु खुद से हिलने को तैयार नहीं होती .

5) पैडल मारना बंद करने के बाद भी साइकिल थोड़ी देर तक चलती है . यह गति का जड़त्व है — साइकिल अपनी गति को बनाए रखती है जब तक घर्षण और हवा उसे रोक न दें .

जडत्व को किसने ढूँढा (who found inertia)

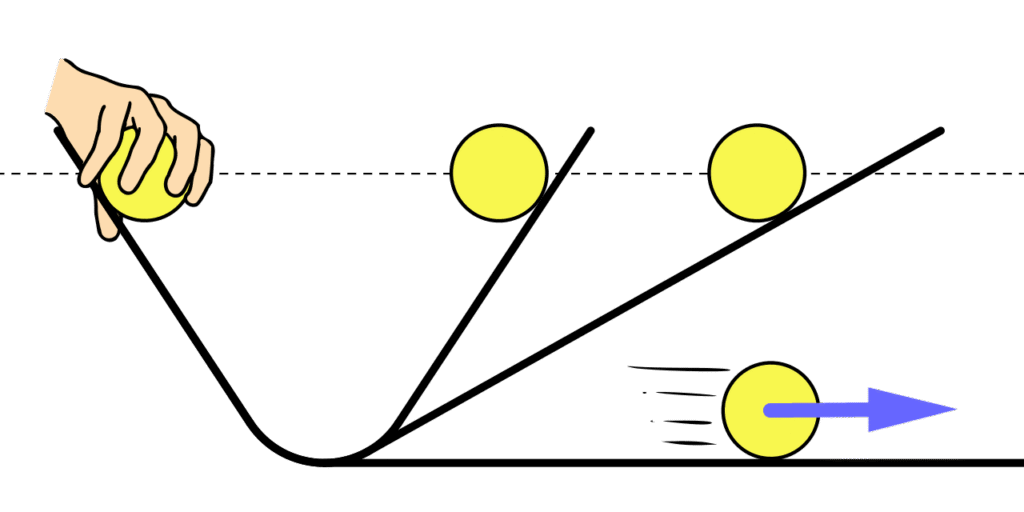
जड़त्व का विचार सबसे पहले वैज्ञानिक गैलीलियो गैलीली ने प्रस्तुत किया था . Galileo Galilei ने inertia को समझाने के लिए झुकी हुई सतह के साथ अपना प्रयोग किया . दो झुकी हुई सतह एक दुसरे के एकदम सामने थी जैसा हम ऊपर की इमेज में देख सकते है . कुछ उचाई से एक सतह से गेंद छोड़ने के बाद गेंद दूसरी सतह पर बिलकुल उसी उचाई पर जाती है , जिस उचाई से गेंद को छोड़ा गया था .

जब दूसरी सतह का झुकाव और कम किया जाता है जैसे इमेज में दिखाया गया है . Galileo Galilei ने पाया की गेंद अभी भी उतनी ही उचाई पर जाती है , जितनी उचाई से गेंद को छोड़ा गया है . लेकिन यहाँ गेंद को उस उचाई तक पोहचने के लिए थोड़ा ज्यादा अंतर की यात्रा (travel) करनी पड़ती है .

इसके बाद Galileo Galilei ने दूसरी झुकी सतह को हटा दिया . अब जब एक उचाई से गेंद को छोड़ा जाता है गेंद को उसी उचाई तक पोहचने के लिए अनंत (infinity ) तक सफ़र करना होगा .

लेकिन असलियत में गेंद कुछ दूरी तय करने के बाद रुक जाती है . गैलीलियो गैलीली का मानना था कि वस्तु की गति में रुकावट घर्षण के कारण होती है. घर्षण गेंद की स्पीड धीर धीरे कम कर देता है . जिस वजह से गेंद रुक जाती है .

मोमेंट ऑफ़ इनरशिया क्या होता है ?(what is moment of inertia in simple terms)

मोमेंट ऑफ़ इनरशिया (moment of inertia ) और द्रव्यमान (mass ) दोनों समान भूमिका निभाते है . mass यहाँ पे सीधे लाइन में चलने वाले वस्तु के लिए उपयोग में आता है , वही मोमेंट ऑफ़ इनरशिया जो वस्तु अपने किसी अक्सिक्स (axis) के इर्द गिर्द रोटेट करती उस वस्तु के लिए उपयोग में आता है .

जैसे द्रव्यमान(mass) जितना ज्यादा उतना ही ज्यादा उस वस्तु का inertia रहेगा . यानी उतनी ही ज्यादा वस्तु अपने गति में होने वाले बदलाव को विरोध करेगी . वैसे ही मोमेंट ऑफ़ इनरशिया जितना ज्यादा उतनी ही एक रोटेटिंग ( घुमने वाली वस्तु ) वस्तु अपने रोटेशन में होने वाले बदलाव को विरोध करती है .

आसन भाषा में बोले तो अगर कोई चीज़ घूम रही है, तो वो अपनी घुमने की गति को बनाए रखना चाहती है. और उसमे होने वाले किसी भी बदलाव को विरोध करती है . तो उसी गुण को घूर्णज जड़त्व (Moment of Inertia) कहा जाता है. मोमेंट ऑफ़ इनरशिया घुमने वाले (रोटेटिंग ) वस्तु का गुण है .

मोमेंट ऑफ़ इनरशिया के उदहारण (example of moment of inertia)

घूमती हुई डिस्क – जैसे सीडी, फ्लाईव्हील या ग्राइंडर की प्लेट .जब एक डिस्क अपने केंद्र के चारों ओर घूमती है, तो वह अपनी स्थिति में बदलाव का विरोध करती है.उदाहरण के लिए, सीडी प्लेयर में सीडी जब तेज़ घूमती है, तो उसे अचानक रोकना मुश्किल होता है. इसका कारण यह है कि डिस्क का ज़्यादातर भार उसके केंद्र से दूरी पर फैला होता है, जिससे उसका मोमेंट ऑफ इनर्शिया बढ़ जाता है .

दरवाज़ा – जब हम दरवाज़े को खोलते हैं, तो वह अपने हिंग से घूमता है. अगर दरवाज़ा भारी या लंबा है, तो उसे खोलने में ज़्यादा जोर लगता है. यह इसलिए होता है क्योंकि उसका घूर्णज जड़त्व अधिक होता है, जिससे वह अपनी घूमने की गति में किसी भी बदलाव का विरोध करता है.

फिगर स्केटर – जब स्केटर अपने हाथ फैलाता है या अंदर लेता है तो उसकी घूमने की गति बदलती है. एक स्केटर जब अपने हाथ फैलाकर घूम रहा होता है और फिर हाथ अंदर कर लेता है, तो उसकी घूमने की गति अचानक बढ़ जाती है. यह इस बात का उदाहरण है कि जैसे-जैसे द्रव्यमान (mass) का वितरण केंद्र के करीब आता है, Moment of Inertia कम होता है और गति बढ़ जाती है . यहाँ पे Angular Momentum conserve होती है .

झूला (स्विंग) – जब आप किसी झूले पर बैठकर आगे-पीछे झूलते हैं, तो झूले को शुरुआत में हिलाने में मेहनत लगती है. इसका कारण ये है कि पूरे शरीर और झूले की व्यवस्था का Moment of Inertia ज्यादा होता है . आपका शरीर झूलने की गति में बदलाव का विरोध करता है.

घड़ी का कांटा (Clock Hand) – घड़ी की सुई भले ही बहुत धीरे घूमती हो, लेकिन उसमें भी घूर्णज जड़त्व (Moment of Inertia) मौजूद होता है . सुई की लंबाई और वजन यह तय करते हैं कि उसका घूर्णज जड़त्व कितना होगा, और वह कितनी सहजता से घूम सकेगी. भारी और लंबी सुइयाँ धीरे-धीरे घूमती हैं क्योंकि उनका घूर्णज जड़त्व (Moment of Inertia) अधिक होता है .

फैन का ब्लेड – पंखा जब चालू किया जाता है, तो शुरुआत में धीरे-धीरे घूमता है और फिर गति पकड़ता है. क्योंकि ब्लेड का द्रव्यमान (mass) मोटर से अधिक दूरी पर स्थित होता है, इसलिए उसका घूर्णज जड़त्व (Moment of Inertia) भी अधिक होता है. उसे तेज़ घुमाने के लिए मोटर को अधिक टॉर्क देना पड़ता है.

मोमेंट ऑफ़ इनरशिया का फोर्मुला (moment of inertia formula)

एक पार्टिकल जो एक एक्सिस के इर्द गिर्द घूम रहा है . अगर हमे इस पार्टिकल का मोमेंट ऑफ़ इनरशिया निकालना हो तो उस पार्टिकल की रोटेशन एक्सिस से जितनी दूरी है उसका वर्ग करना पड़ेगा . इस दूरी के वर्ग को पार्टिकल के mass से गुना करने से हमे मोमेंट ऑफ़ इनरशिया (moment of inertia ) मिल जाएगा .

सिंगल पार्टिकल का मोमेंट ऑफ़ इनरशिया निचे दिए गए फार्मूला से निकाला जाता है .

$$I=mr^{2}$$

अगर हमारे पास एक से ज्यादा पार्टिकल हो तो उनका मोमेंट ऑफ़ इनरशिया निचे दिए गए फार्मूला से निकाला जाता है .

$$I=\sum_{}^{}m_{i}r_{i}^{2}$$

m_i यहाँ i नंबर के पार्टिकल का मास (mass) है

r_i यहाँ i नंबर के पार्टिकल की रोटेशन एक्सिस से दूरी है

कुछ और वस्तुओ के मोमेंट ऑफ़ इनरशिया(moment of inertia ) के फोर्मुले निचे दिए गए है .

Object Type	Axis of Rotation Location	Moment of Inertia (I) Formula
Point Mass	At a distance r from axis	I = m × r²
Thin Rod	About center, perpendicular to length	I = (1/12) × M × L²
Thin Rod	About end, perpendicular to length	I = (1/3) × M × L²
Solid Cylinder / Disc	About central axis (through center, flat face)	I = (1/2) × M × R²
Hollow Cylinder	About central axis (through center, flat face)	I = M × R²
Solid Sphere	About diameter (through center)	I = (2/5) × M × R²
Thin Spherical Shell	About diameter (through center)	I = (2/3) × M × R²
Rectangular Plate	About center, perpendicular to surface	I = (1/12) × M × (a² + b²)